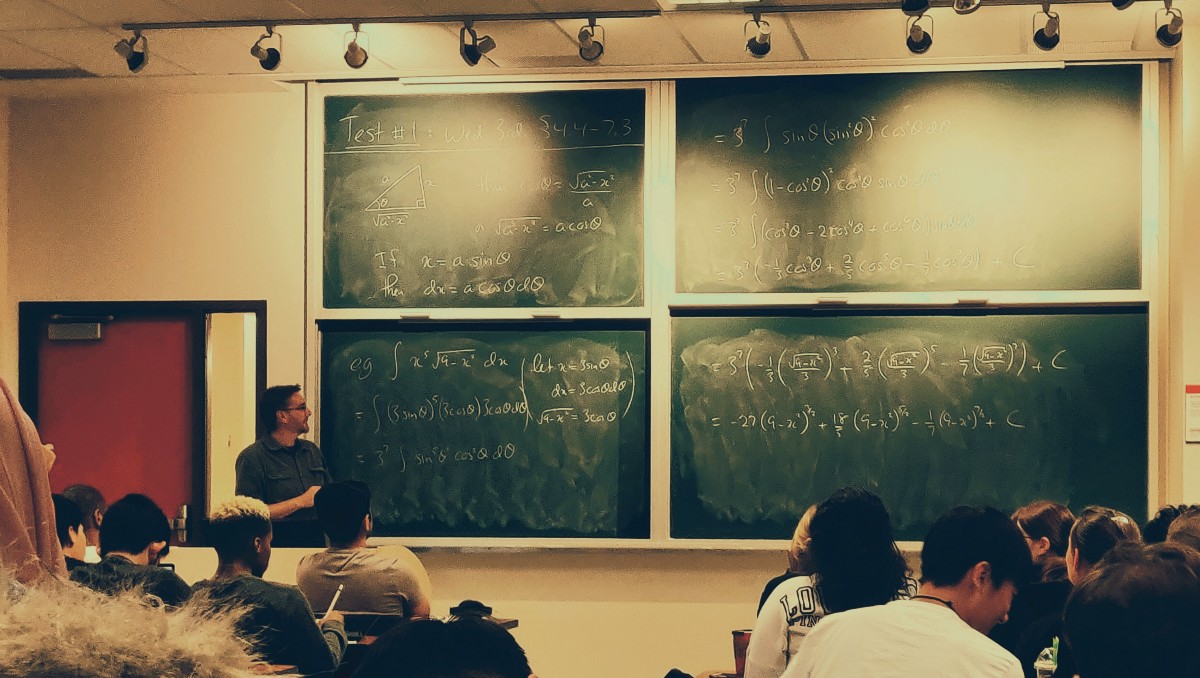Or, looking for data and boundary conditions
Engineering problems are typically well-bounded. That is, we only need to solve for particular conditions, and problems often give us the values of critical variables.
Undergraduate engineering problem-solving lies less in mathematical derivation and more in recognizing the shape of a problem, which means identifying the right mathematical or physical constants, correctly using boundary conditions, and selecting the right methodological approaches to derive a solution.
We can take a similar approach in real life, and pretty soon, you’ll get in the habit of analyzing problems and extracting the relevant parts.
📊 Find the data
The first thing to strip out of a potential problem is its data. In the fluid mechanics example, we have several fixed variables:
- the density and viscosity of the upper layer of freshwater
- The density and viscosity of the lower layer of saltwater
- The width of the channel
- The height of the channel for each layer of water
- The volumetric flow rate of water of the upper layer
In other problems, we might be given values for the physical constants we’ll need to solve the problem or to derive some desired result.
So far, so boring. Am I right?
Well, yes, that’s true. But wait — there’s more! These values are just data. Facts. When you’ve done hundreds of engineering problems, you start skimming for data. It becomes second nature. Ask questions, find the data.
Some problems, like the engineering example, come to you with canned facts:
- Attrition in the team is 10% per year, and average tenure is nine months.
- Customer churn is 3% per month.
- Support calls are up 7% this quarter, and the average resolution time has increased to 3 days.
If you do get data, question it. I rarely trust it at the outset. We misunderstand a lot of data, and sometimes it’s incorrectly computed or biased.
When you don’t get data for free
If you think there’s a problem but don’t have much hard evidence, hit pause. A lot of “problems” are hypotheses (generally of two flavors: if we do a, then b or x is happening, because y), informed by common sense, observation, or accumulated experience, but little data.
Consider the problem example from earlier in the article:
Car owners in major northern cities struggle to get winter tires installed on time because traveling to service centers is inconvenient and time-consuming, and appointments are usually booked months in advance. How might we make winter tire installation more convenient?
This situation sounds reasonable, but is it true? You don’t have any data. But whether it’s a true problem that people are willing to pay to solve is unknown. You might end up with two hypotheses: one positing why the problem is occurring (x because y) and then another when you want to test a solution (if a, then b).
You need to do your research to understand why the problem exists. When you don’t have much data early on, ask yourself: what questions do I need answers to? How might I answer those questions?
For this example, we could figure out things like:
- What percent of households have a car
- How many snow days specific cities have, on average, per year, and what is the probability of snow falling (e.g., prompting people to think of snow tires) at different times of the year
- How many service centers are within a 10-minute radius of a given neighborhood
- How far people are willing to travel to get their tires changes
This data might support the theory that most people struggle to get their winter tires installed on time because of the inconvenience of traveling to service centers. You’d be able to rewrite the problem statement, using evidence to support the assertion.
🔒 Define the boundary condition
The next thing you need to do after identifying available or easy-to-acquire data points is to identify your boundary conditions—or constraints. Every problem has constraints, and without them, you probably won’t succeed. In fact, with them, you might thrive.
In engineering problems, these are called boundary conditions. Boundary conditions are constraints that must be true. In the fluid mechanics example, we know that the top surface of the upper layer is exposed to the air. Therefore, the force acting at any one point at the very top is zero, and the shear stress (essentially, pressure perpendicular to the surface of the water) is also zero.
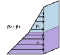
We also know that the velocity of the water at the bottom of the channel is zero, because of something called the no-slip condition. This is given in the problem itself:
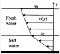
With these conditions known (along with the fact that the flow is “steady,” e.g., a continuous force acts upon the flow upstream and outside the bounds of the problem), we are on the way to solving the problem. Without these boundary conditions, we’d need to account for more variables in our equations, and might struggle to solve the problem. For instance, if the problem stated “a steady wind acts on the top surface of the water,” without giving us the magnitude of the stress exerted by the wind, we’d be screwed.
Scanning your problem for constraints
In the Donlands subway station example, we’d face many constraints. For example:
- Two houses occupy the most viable location for a new subway entrance
- Soil conditions on the site may require remediation
- The deadline for construction to begin to qualify for provincial funding
At this point, you’ve defined the problem, surfaced the most important relevant data that supports it, and have identified constraints that inform your approach to solving it. Things are humming along.